BEN2のブログ

たまに書いています。

ABC 158 E - Divisible Substring

競技プログラミング

ABC 158 E - Divisible Substring に関連する、合同式の性質 (除法) についてのメモを残します。

合同式の性質 (除法)

入力例 1 : N = 4、 P = 3、 S = 3543 について考える。
下図のような配列 A を用意する。

f:id:BEN2suzuka:20200308114449p:plain

S の連続する部分文字列について、
たとえば、54 は \displaystyle \frac{A [ 3 ] - A [ 1 ]}{10^{1}}、354 は \displaystyle \frac{A [ 4 ] - A [ 1 ]}{10^{1}}、35 は \displaystyle \frac{A [ 4 ] - A [ 2 ]}{10^{2}} と表すことができる。
求めたいものは、

\begin{aligned} \frac{A [ l ] - A [ r ]}{10^{r}} \equiv 0 \, ({\rm{mod}} \, P) \end{aligned}

を満たす組 (l, \, r) の総数である。

10 と P が互いに素のとき、

\begin{aligned} A [ l ] - A [ r ] \equiv 0 \, ({\rm{mod}} \, P) \Leftrightarrow \frac{A [ l ] - A [ r ]}{10^{r}} \equiv 0 \, ({\rm{mod}} \, P) \end{aligned}

であるから、

\begin{aligned} A [ l ] - A [ r ] \equiv 0 \, ({\rm{mod}} \, P) \end{aligned}

を満たす組 (l, \, r) の総数を求めればよい。シンプルになった。

合同式の性質 (除法) :
m と p が互いに素であるとき、 ma \equiv mb \, ({\rm{mod}} \, p) \Leftrightarrow a \equiv b \, ({\rm{mod}} \, p)

しかし、10 と P が互いに素でないとき、すなわち P = 2, 5 のときは、

\begin{aligned} A [ l ] - A [ r ] \equiv 0 \, ({\rm{mod}} \, P) \Rightarrow \frac{A [ l ] - A [ r ]}{10^{r}} \equiv 0 \, ({\rm{mod}} \, P) \end{aligned}

は一般には成り立たない。
ただ、これらのときは部分文字列の下一桁に注目することで、 P で割り切れるかどうかを判定できる。
下一桁が偶数ならば 2 の倍数。下一桁が 0 または 5 ならば 5 の倍数。
これを使えばよい。

では、10 と P が互いに素のときについて、 A [ l ] - A [ r ] \equiv 0 \, ({\rm{mod}} \, P) を満たす (l, \, r) の総数を求めたい。
配列 A について {\rm{mod}} \, P をとる。

f:id:BEN2suzuka:20200308120538p:plain

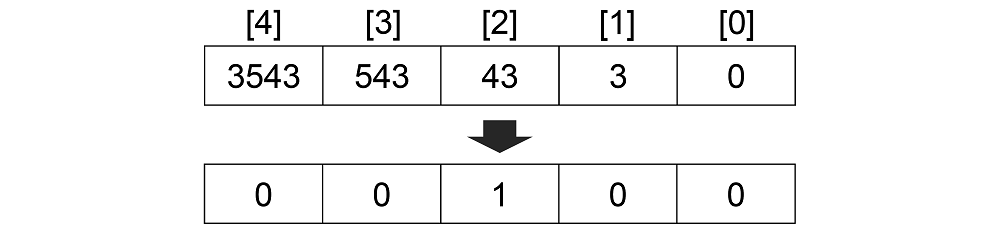
実装を見ると、たとえば 543 を P で割った余りを求めるときは、 543 = 5 \times 10^{2} + 43 と分解して考えていることがわかる。

\begin{aligned} A [ l ] - A [ r ] \equiv 0 \, ({\rm{mod}} \, P) \Leftrightarrow A [ l ] \equiv A [ r ] \, ({\rm{mod}} \, P) \end{aligned}

であるから、 A [ i ] \, ({\rm{mod}} \, P) の等しい 2 つの要素を選ぶ方法の総数を求めるとよい。

コードは、YouTube 解説放送 を参考に。

#include <bits/stdc++.h>
using namespace std;

int main() {
  int N, P; cin >> N >> P;
  string S; cin >> S;
  long long ans = 0;
  if (10 % P == 0) {  // P が 2, 5 のとき
    for (int i = 0; i < N; i++) {
      if ((S.at(i) - '0') % P == 0) ans += i+1;
    }
  }
  else {
    vector<int> A(N+1, 0);
    int ten = 1;
    for (int i = N-1; i >= 0; i--) {
      int tmp = (S.at(i) - '0') * ten % P;  // S[i] * 10**r
      A.at(i) = (A.at(i+1) + tmp) % P;
      ten *= 10;
      ten %= P;
    }
    map<int, long long> M;
    for (int i = 0; i < N+1; i++) {
      if (M.count(A.at(i))) M[A.at(i)]++;
      else M[A.at(i)] = 1;
    }
    for (auto p : M) ans += (p.second * (p.second - 1)) / 2;
  }
  cout << ans << endl;
}